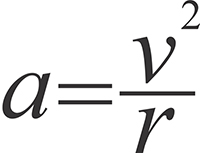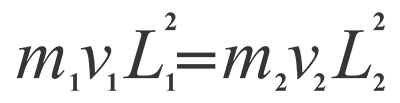OpenSpace 5
| Title: Place Title Here | ||
|
[Cover Img] |
About:
|
Tags:
|
Space Catapult
Author: Mr. Giorgi Lobzhanidze
Address: Tbilisi, Republic of Georgia, Europe
Email: mailto:giorgi9@gmail.com
INTRODUCTION
The new method for sending the spacecrafts in deep space is presented here. The paper describes the long rod rotated by electro motor placed at the Space Elevator’s counterweight and at Lagrangian points. This simple structure will enable the rod to gain high velocity and carry the payload with it. After reaching the desired speed the rod will release the payload that will fly in space along the imaginary circle’s tangent. This structure we called Space Catapult and it should work with the assist of Space Elevator. This latter should be used for carrying the payload from the Earth to Space Catapult’s rod.
For exploring the outer space the humankind generally uses the rocket engines, mostly chemical-propelled ones. They enable us the explore near-Earth celestial bodies and other planets in the solar system. They even enabled us to send several deep space missions beyond the solar system such as Pioneer-10, Pioneer-11, Voyager-1, Voyager-2, however by means of this technology the flight lasts undesirably long and it seems to be impossible to reach remote celestial bodies in space such as stars, so new technologies are necessary for this purpose. However new technologies do not necessary imply new kind of rocket engines, such as Ion Drives because they are capable for gaining several ten times higher speeds only, but for remote celestial bodies even they are not suitable. Besides, they need a huge amount of energy to be stored onboard the spacecraft and this will make additional problems. So, high speed should be achieved with absolutely different approach. How this can be done?
High speed can be easily achieved by means of fast-rotating rod around the electric motor. The motor’s rotational speed can be very high; the rod also can be quite long, hence the rod’s end’s linear speed can be extremely high, absolutely unachievable for any other technologies nowadays. The payload should be fastened at the rod’s end where the linear speed generally reaches maximal value. After reaching the necessary speed the rod will release the payload that will fly along the tangent from the current position. Thus the electric energy can be turned into payload’s speed and its velocity could be as high as we wish (except the speed of light of course). In principle the Space Catapult (thus we call this structure) would be the simplest, the most convenient and direct way for converting the energy/electricity into speed and conveying it to payload.
As we see the Space Catapult is quite uncomplicated structure, however if we wish to gain high speeds we should deploy it in space, not on the Earth. Indeed, our planet is surrounded with dense atmosphere that impedes any quick motion, so if we rotate the rod quickly the atmospheric drag and generated heat would burn it very soon, therefore the Space Catapult should be built and deployed in space only, and as we suppose-at the Space Elevator’s counterweight. In other words, the Space Elevator’s counterweight will operate as Space Catapult. See image below:
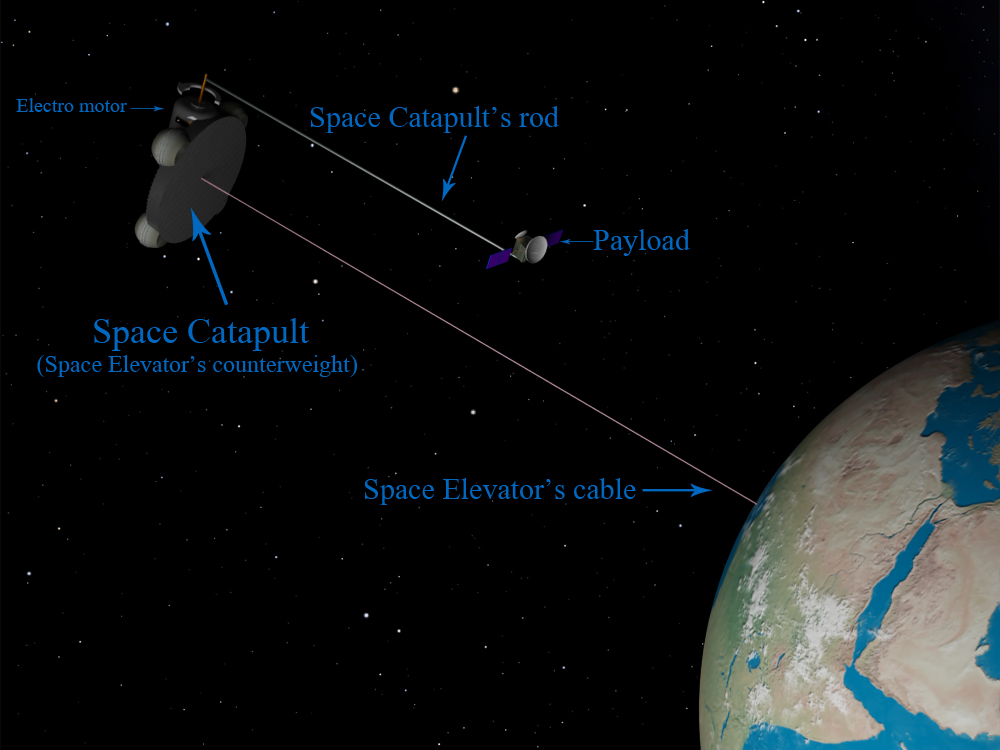 Generally, what is the Space Elevator 1 2? According to modern concepts it will be the tall vertical structure built on equator and will have height of several ten thousand kilometers with its thin cable fastened to the base station on the Earth and with counterweight placed higher geostationary orbit. Because of balance between centrifugal force and gravity this structure will be stretched and the cabin will move along its cable carrying the goods into high orbit. After delivering the payload, the cabin will descend and carry the next one.
In Space Elevator’s concepts several solutions have been proposed to act as a counterweight:
Generally, what is the Space Elevator 1 2? According to modern concepts it will be the tall vertical structure built on equator and will have height of several ten thousand kilometers with its thin cable fastened to the base station on the Earth and with counterweight placed higher geostationary orbit. Because of balance between centrifugal force and gravity this structure will be stretched and the cabin will move along its cable carrying the goods into high orbit. After delivering the payload, the cabin will descend and carry the next one.
In Space Elevator’s concepts several solutions have been proposed to act as a counterweight:
1. Heavy, captured asteroid
2. Space dock, space station or spaceport positioned past geostationary orbit
3. Extension of the cable itself far beyond geostationary orbit.
The third idea has gained more support in recent years due to the relative simplicity of the task and the fact that a payload that went to the end of the counterweight-cable would acquire considerable velocity relative to the Earth, allowing it to be launched into interplanetary space. However this idea cannot be completely shared by us due to following reason:
It is well-known that the values of both Orbital and Escape Velocities decreases with increasing the altitude while the tangential velocity of Space Elevator’s cable increases. We can see the differences between them from the chart presented below:
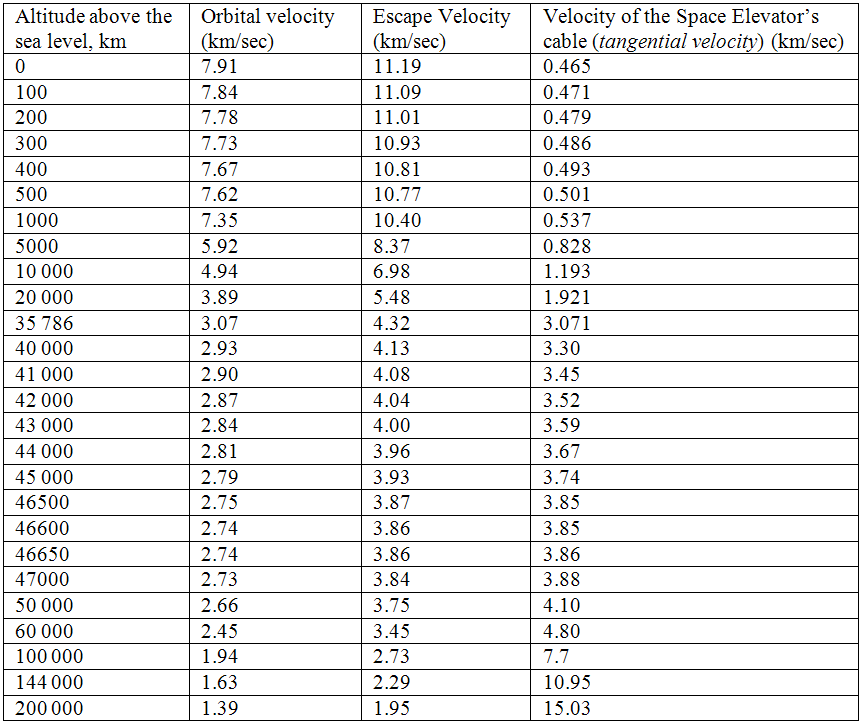
As we see from this chart the tangential velocity of the Space Elevator even at its end (144 000 or 200 000 km altitude) is not very high to decrease the necessary time for covering the distance from the Earth to remote celestial bodies significantly. To achieve this, even the longer Space Elevator would be needed (its tangential velocity is directly proportional to its length) and this circumstance would complicate the technical task for building such Space Elevator. Because of this, there is no necessity to extend the cable itself far beyond geostationary orbit as proposed in the third variant. In any case, we have already seen that by means of Space Catapult it is possible to gain such huge velocities that are absolutely unachievable with other technologies, for example with Space Elevator. Therefore, using the counterweight and placing the Space Catapult there definitely has got some technical sense.
However, we think that the question where the Space Catapult should be placed needs further discussion. Theoretically, the Space Catapult with its payload and nuclear reactor/solar panel needed for rotating the rod may be mounted not only at the counterweight, but on the Space Elevator’s cabin also that can carry all these goods to space in a usual way, as it should do it according to Space Elevator’s modern concepts. This option is quite possible, however for realizing this we need to know the mass of the payload, nuclear reactor/solar panels’ mass plus Space Catapult’s mass from one hand and Space Elevator’s lifting capacity (this must be more) from other hand, but these data are not available nowadays, therefore we think that the Space Catapult should be still mounted at the Space Elevator’s counterweight where it will be possible to send the payloads into deep space in continuous mode at high velocities.
As we saw the Space Catapult is capable to gain very high velocities; however there is being developed other technologies and they in future will enable the spacecraft to fly at high speeds in space. These are Ion Drive systems, more precisely the most perspective one-Variable Specific Impulse Magnetoplasma Rocket (VASIMR) which still under development can be used in future for deep space missions. Can these engines and Space Catapult be the rivals in space? Since none of them have been built and used in space yet we cannot give a persuasive answer to this question; however still it is possible to underline Space Catapult’s one significant advantage: if the future spacecraft uses the VASIMR (or any other kind of Ion Drive) engine it will definitely need to be equipped with nuclear reactor, otherwise the spacecraft will not be able to gain high speeds, also it will need to carry fuel tanks for this purpose. As for the Space Catapult, it can give much higher speed to spacecraft, besides it will have stationery power plant (see Energy source placed on the Space Elevator’s counterweight) at the Space Elevator’s counterweight, so the payload will not have to carry the nuclear reactor onboard and this circumstance will lighten the work for deep space spacecraft. Besides, we should not forget that unlike the spacecrafts equipped with ion drive engines the Space Catapult will need no fuel for gaining high velocities.
Briefly, Space Catapult’s advantages over any kind of propulsion systems are:
1. Ability to gain any speed that is absolutely unachievable by means of other kinds of engines.
2. No need by spacecraft to carry energy source that would make it too heavy and impracticable.
The Space Catapult needs long rod
When building the Space Catapult at Space Elevator’s counterweight we should install quite long rod there, the shorter the rod is, the easier would be installing it, however we should note that rod cannot be extremely short, let’s say 1 km length or so due to following reason:
When we are going to send some payload into space, we need not only high velocity, but one certain direction also. The little inaccuracy in direction, inclination in several arcminutes is actually acceptable since the spacecraft would easily balance it with its engines; however great inclination from the initial direction would send the spacecraft into the completely different direction and in such case the whole mission will fail.
If two Space Catapult’s rods have the length of let’s say 1 kilometer and 10 kilometers, then for giving to payload some certain linear speed (for instance 100 km/sec) these rods should rotate at different angular velocity. It is easy to ascertain that the shorter rod should rotate 10 times faster to gain the same linear speed than the rod with more length. But the faster the rod rotates, the more difficult will be to “catch” the needed moment for releasing the payload from the rod for sending it towards some certain direction. If the rod is too short, then it has to rotate very quickly for gaining some certain linear speed and therefore it will be extremely difficult catching the needed moment for releasing the payload. Hence, too short rod can make problem for sending the payload to some certain direction in space especially at high velocities. So, based on payload’s needed velocity we should find rod’s desired, minimal length that will enable us to send the payload in space to necessary direction without fear that it may yaw from the course.
However, rod’s length will be crucial for payload’s abilities for withstanding the acceleration also. As an example, we can try to calculate its value which the payload will have to withstand during rod’s rotation. The acceleration of the body rotating at the circle with some constant velocity is calculated by the following formula:
Where a is acceleration in m/sec2, v is payload’s linear velocity on the circle in m/sec and r is radius of the circle in meters, in our case it is equal to rod’s length. Let’s assume that the rod is 100 km length and the electromotor rotates it so that payload’s speed is equal to 50 km/sec, in this case acceleration will be equal to 25 000 m/sec2, which is about 2550 g. The modern technologies enable to design and manufacture the spacecraft’s subsystems (avionic and etc.) capable to withstand such acceleration. This circumstance somehow restricts the speeds that we can achieve, in any case their values actually depends on spacecrafts’ abilities for withstanding g-loads. But what can we do if much higher speeds are needed? The answer directly derives from that formula: the radius should be more; by the way note that this is additional reason why the longer rod is more useful. If we are able to make the extra long rod, then this will enable us to gain much higher velocities.
What material should be used for manufacturing the rod? It is obvious that if very high speeds are needed the rod should be long and even in this case the acceleration at its end will be quite high, therefore sufficiently strong and light materials are needed for this purpose and making them is as similar challenge as in case of Space Elevator where the same requirements arises for the cable’s material. The lightness is needed because in case of heavy rod a lot of energy will be needed to rotate it; the strength is needed because in case of lack this property the rod will be destroyed due to great acceleration.
The mechanism for holding and releasing the payload
How the payload can be held by Space Catapult’s rod during rotation and how it can be released from the rod? We think that using electromagnet plus mechanical holding devices would be a good solution. More precisely, after the payload is attached to the rod it must be held by means of both methods until the rod accelerates and reaches necessary velocity (it may take even several days), but with approaching the desired speed the mechanical device should release the payload however the electromagnet(s) should still hold it. The explanation of such approach is following: generally the mechanical devices are much slower/sluggish in performance than electronic ones. We have already said that when releasing the payload the extreme accuracy is needed and mechanical devices cannot guarantee the exact time of releasing the payload unlike electronic ones. That is, it’s unlikely that mechanical devices can release the payload at some certain moment when needed while in case of electromagnet it would be enough to cease electric current there, it would lead to immediate vanishing of the magnetic field and sending the payload along the tangent from the point where the payload would be at the current moment.
We think that the fastest control system would enable to release the payload to certain direction. This system (extremely fast-operating computer plus measuring equipments) should know the current position of the rod’s end, the current speed, the needed direction and be capable for computing the necessary moment for giving the order for diminishing the voltage for electromagnets and hence releasing the payload to desired direction and velocity.
Rod’s plane of rotation towards the Earth
The Space Catapult’s rod when rotating makes the circular plane/flatness in space and this plane may be horizontal/parallel to Earth surface, that is making the right angle to Space Elevator’s cable or it may be placed along the cable; see the both possible situations here:
Both approaches have got their advantages/disadvantages and here we will discuss this question, first of all from the point of view of safety.
For gaining extremely high velocities quite long rod would be needed, maybe with the length of several thousand kilometers or even more. If such rod is placed along the Space Elevator’s cable then the rod during rotation will cross many orbits from the Medium Earth Orbit to High ones. When rotating, the rod may actually hit any satellite and/or space debris object and such collision can lead to rod’s complete destruction; therefore we should choose such plane which would be much more free from any artificial objects; hence if the rod rotates horizontally/parallel to Earth’s surface at high enough altitude where the satellites’ population is relatively low then this measurement would justify itself because under such circumstance the rod will not cross satellites’ orbits (rod’s plane of rotation will simply coincide to one orbit’s path). However, we should also note that this altitude actually depends on the Space Elevator’s proposed length. Indeed, the Space Catapult’s rod should be mounted at the Space Elevator’s counterweight; this counterweight from its side should be placed at the end of the Space Elevator at such altitude where the satellites’ population is as low as possible. This means that Space Elevator’s proposed height should be agreed with mounting Space Catapult on its counterweight. According to various databases the number of man-made objects at high orbits, more precisely beyond geostationary orbit is much less than on the lower orbits 3 4 5 6, therefore the Space Catapult with its rod should be located at the altitude of 50 000-60 000 km above the sea level. At such altitude the space is almost free and nothing will impede rod’s rapid rotation. Besides, the satellites at high orbits are orbiting around the Earth slower than on the lower orbits (as known any satellite orbits around its primary body slower in apogee than in perigee), therefore if some tracking system is mounted at Space Elevator’s counterweight then it will enable the Space Catapult to avoid undesired collision with satellites during Space Catapult’s performance. In other words, the Space Catapult should operate only when the there are no satellites near its vicinities.
Now we will try to discuss this question from other side.
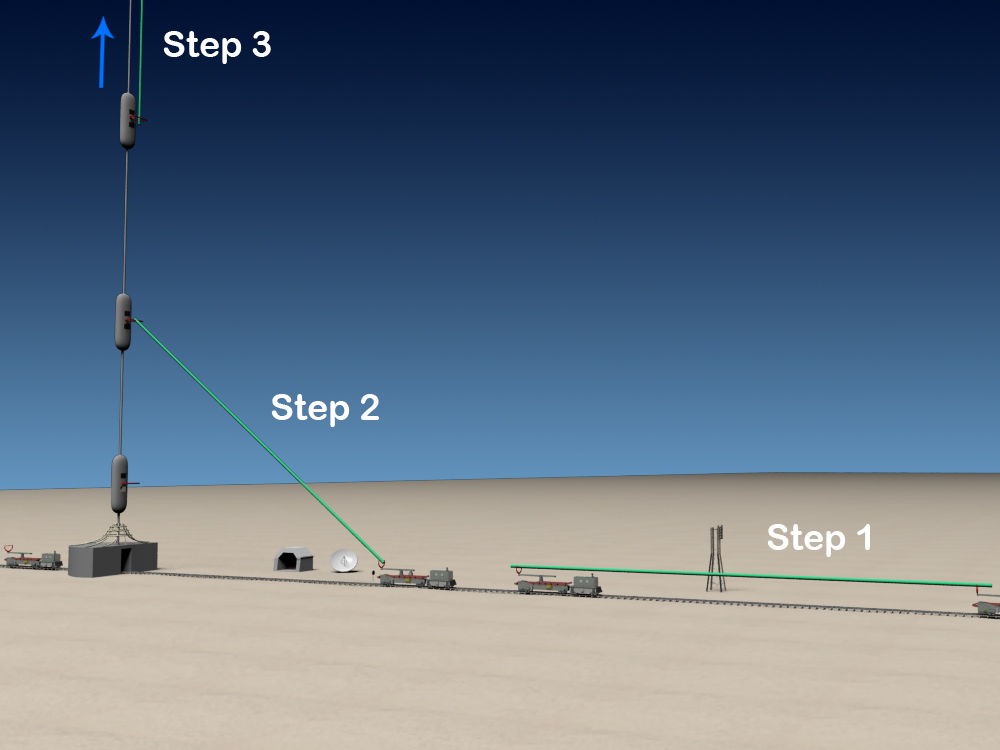
How the payload can be transferred from the Space Elevator’s cabin to the Space Catapult’s rod? One way is following: cabin reaches the counterweight where the payload will be released, then payload will be mechanically conveyed to rod, continues its way on the rod (like the train rides on the rails) and after reaching rod’s end it stops, the rod begins rotating and after gaining necessary linear speed it releases the payload to needed direction. This method is generally realizable; however it seems to be too complicated and unpromising compare to the second one: the Space Catapult’s rod is stopped in space so that it to be directed downwards to the Earth and be parallel to Space Elevator’s cable. The Space Elevator’s cabin moving along the cable with payload stops at the cable near the end of the Space Catapult’s rod and releases the payload that will fly to the rod, attaches itself to the rod’s end (here the electromagnets would be useful), the rod begins rotating and after gaining needed linear speed will release the payload to necessary direction.
This second way seems to be more promising because the first one is much more complicated as we have already said: first of all there would be needed some mechanical devices for transferring the payload from the Space Elevator’s cabin to counterweight, the counterweight should have the hole for the payload to move through it from below (we should not forget that the Space Catapult should be mounted at the counterweight, not beneath it), besides the rod should be made so that it to have some conveying surface (rails for instance) the payload to move on it. As we see it would be much more convenient if it is possible to convey the payload from the cabin to the rod directly and this would be feasible under the second method which is depicted below:
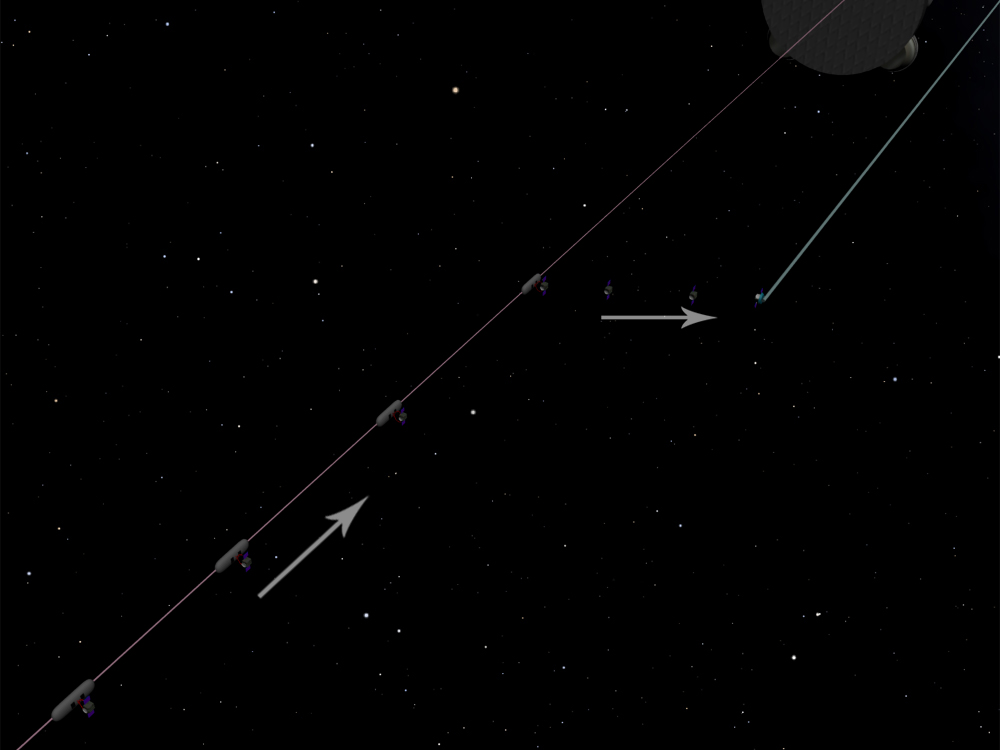
One more aspect regarding Space Catapult’s position. This structure, its rod, its electro motor and etc should be mounted at Space Elevator’s counterweight so that the rod to be placed westwards from the cable. The reason of it is following: when the Space Elevator’s cabin stops and releases the payload (which should fly to Space Catapult’s rod) the current speed of which will/should be more than the value of the Orbital/Escape Velocity at the current altitude. After releasing the payload will fly westwards and upwards because its orbit will be ellipse, under ellipse the payload will fly higher to apogee and at the speed less than Space Elevator’s current speed at the given altitude, in other words the released payload will “lag behind” the Space Elevator’s cable; therefore payloads’ stopping points at the cable and Space Catapult’s rod’s length should be calculated and chosen so that the payload to fly directly towards rod’s end. This process would be feasible in both cases-if the rod’s plane of rotation is parallel to Earth’s surface and if it is placed along the cable-but still this would be easier for the payload to achieve the rod’s end if the rod is placed along the cable because at least the distance that the payload should cover in space will be less.
The length of the Space Catapult’s rod placed at the Space Elevator’s counterweight might vary since for various spaceflight purposes different initial speed will be needed and relatively low speed could be achieved by means of shorter rod. Because of this reason it might be necessary to change Space Catapult’s rod’s length, therefore it would be useful if the rod consists of two parts where the first part would be perpetually attached to electro motor and the second one will be attached to the first part if necessary. For this operation Space Catapult’s rod should be placed along the cable since the relative nearness would make this operation quite easy and it could be accomplished by the crew directly from the Space Elevator’s cabin stopped at the needed altitude.
For deciding the question how the Space Catapult’s rod should be placed towards the Space Elevator’s cable we should take into consideration one substantial circumstance-to which direction do we plan to send the payload in space by means of Space Catapult? This circumstance will influence deciding this problem due to following reason:
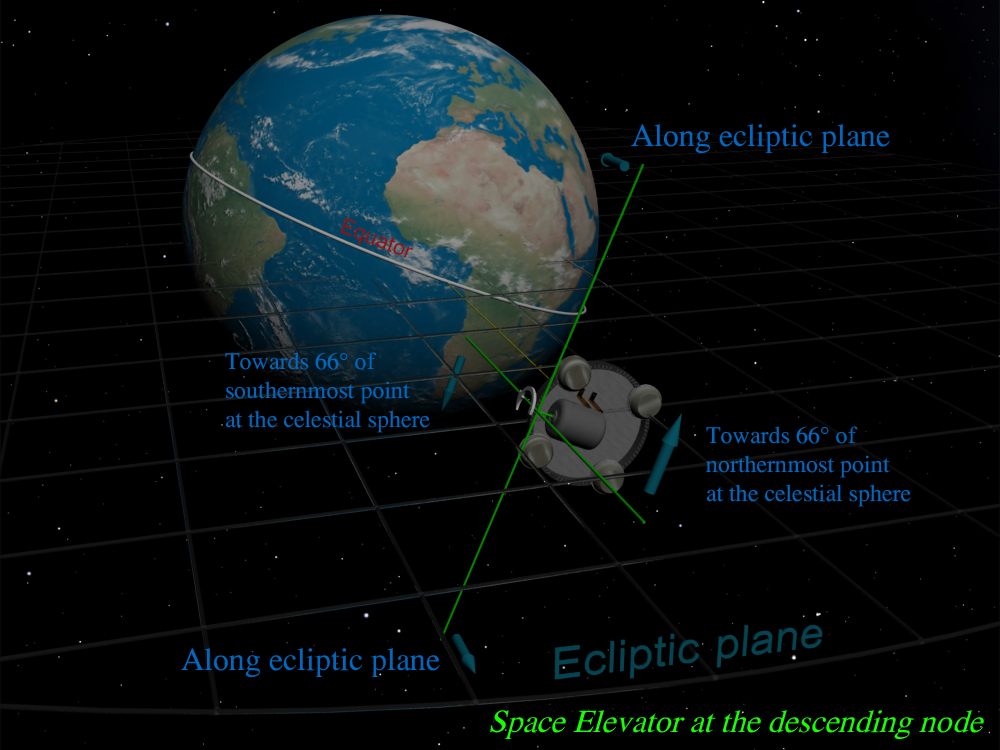
In case if Space Catapult’s rod is parallel to Space Elevator’s cable and if rod’s plane of rotation is parallel to Earth equator, then this plane will be orthogonal to Earth’s rotation axis. This axis from its side is tilted to ecliptic plane by 66° 34'. This means that Space Catapult’s rod’s plane of rotation will be tilted to ecliptic plane by 23°26'. Here follows very important consequence: under above-mentioned conditions the rod when rotating will be capable for covering only the part of the celestial sphere from 0° to 23°26' (counted from ecliptic plane northwards and southwards to Ecliptic poles). This is about one fourth of the celestial sphere (23°/90°), this will not make problems if we intend to use the Space Catapult for exploring the solar system’s planets because their orbits’ tilts towards ecliptic plane do not exceed 7° (for planet Mercury, for other planets this tilt is even less); however we will not be able to send the payload for example to the nearest star Alpha Centaurs because this star is located at -42 degree according to ecliptic coordinate system in the celestial sphere.
The situation will drastically change if Space Catapult’s rod is parallel to Space Elevator’s cable and if rod’s plane of rotation is orthogonal to Earth’s equator and therefore parallel to Earth’s axis of rotation. We have already discussed this option when we mentioned that the rod should be placed westwards from the cable and explained why it would be useful-for delivering the payload from Space Elevator’s cabin to Space Catapult’s rod. Under such conditions the Space Catapult will be capable to aim to any point on the celestial sphere. Indeed, the Earth with the Space Elevator rotates around its axis and Space Elevator’s counterweight draws an imaginary circle in space. This circle is tilted to ecliptic plane at 23°26' and crosses this plane in two point called ascending and descending nodes. The other points that are 90° away from these nodes we call point(s) of maximum elevation/depression (relative to ecliptic plane). When the Space Elevator is at ascending/descending node its rod and hence the payload can be directed to any point from 0º to 66º on the celestial sphere northwards and southwards from ecliptic plane. This makes about 75 % of celestial sphere. See the image depicting this situation:
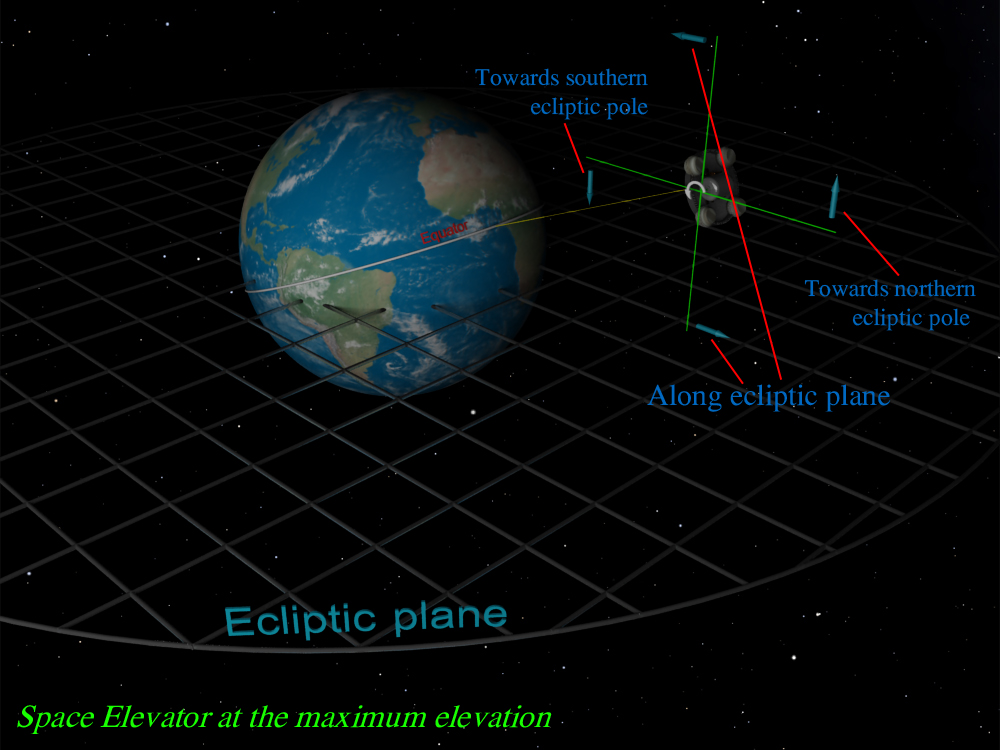
But when the space Elevator reaches the points of maximum elevation/depression then its rod during rapid rotation may be directed to any point from southern Ecliptic pole to Northern pole at the celestial sphere because at these points rod’s plane of rotation is orthogonal to ecliptic plane and thus the rotating rod can aim to ecliptic poles as well as other points. See this situation below:
The situation will be similar if the Space Catapult’s rod is orthogonally placed towards cable. Under such approach Space Catapult’s rod’s plane of rotation will be tilted to ecliptic plane by 66° 34' and the Space Catapult will be capable to cover three fourths (66°/90°) of the celestial sphere when the Space Elevator is at the points of maximum elevation/depression and the whole celestial sphere when the Space Elevator is at ascending/descending nodes. For aiming the needed point on the celestial sphere the Earth should occupy the appropriate attitude towards the stars during the revolution around its axis, the same thing should be done under previous case described in the paragraph above.
In conclusion, thinking about rod’s plane of rotation towards the Earth, we should note one important difference between above-mentioned approaches: if Space Catapult’s rod’s plane of rotation is parallel to Space Elevator’s cable, then in case of emergency during Space Catapult’s performance (for example if the Space Catapult’s rod is cut by sudden meteorite bombardment) the rod’s part with the payload may simply crash to the Earth at huge velocity if the rod at this moment is directed to the Earth. This cannot happen if Space Catapult’s rod’s plane of rotation is orthogonal to Space Elevator’s cable because payload’s rotational path will not be directed towards the Earth and hence its flying trajectory will never cross the Earth.
Braking the Space Catapult’s rod
After releasing the payload at necessary speed and direction, the Space Catapult’s rod will have a huge angular velocity that needs to be decreased to zero in order the Space Catapult’s rod to get another payload in motionless position and then to send it to space. What methods can we use to reduce Space Catapult’s rod’s rotation to zero? There are several possible ways:
1. The electromotor designed for accelerating the rod may actually play a role of brakes, more precisely after releasing the payload to space the electromotor should operate/rotate in the opposite direction, hence rod’s rotational speed will be diminished to zero after that electromotor will stop operating. Under such method a bit less energy will be spent for decelerating the rod than in case of accelerating because when decelerating the rod is free from payload.
2. An ordinary mechanical brakes, however due to electro motor’s and rod’s sizes a huge brake(s) would be needed to be installed on the Space Elevator’s counterweight and this circumstance would make additional problems from the engineering point of view. Nevertheless, we should admit that under such method we would not need as much energy as during accelerating; on the contrary, in this process the heat will be emitted as it generally happens during braking.
3. For decelerating the rod we can use the well-known phenomenon in physics-electromagnetic induction: when the conductor/ closed circuit moves into the magnetic field the electric current is generated there. In case of Space Catapult we can use this phenomenon in the following manner: the conductor should be wrapped around the whole length of the rod like a helix and there should be possibility that this conductor to be turned into the closed circuit by means of mechanically connecting its ends (see the image below). After releasing the payload at necessary speed and direction this circuit should be closed, then according to electromagnetic induction the electric current will be generated in the conductor and the energy of this electric current will come from rod’s kinetic energy. Therefore, inducted electric current in the enclosed circuit will force this circuit and rod to lose kinetic energy and speed. The part of the generated electric current will be spent in prevailing conductor’s electric resistance:
The advantage of this method is that for decelerating the rod no energy will be required, as for drawback-much time will be required for this purpose because at the altitude of several ten thousand kilometers the Earth’s magnetic field is quite weak and the effect described in the paragraph above will need much time to operate and give necessary result.
4. The above-described third method could be realized in a bit different way: if the conductor wrapped around the rod is a closed circuit and if we conduct the electricity there then the electric current will generate its own magnetic field that will counteract with Earth’s one. More precisely, according to Lenz's law induced current’s magnetic field will be in such a direction as to oppose the motion or change causing it, in other words induced current’s magnetic field will counteract outer magnetic field’s any change and this will cause decelerating rod’s rotation and finally its stopping.
5. The obvious disadvantage of the third and fourth method described above is weakness of the Earth’s magnetic field because of which decelerating the rod may be delayed in time. For solving this problem we can create artificial magnetic field by means of electromagnets. Particularly, one electromagnet should be placed at the Space Elevator’s counterweight, very close to Space Catapult’s rod. The second electromagnet should be placed directly on the Space Catapult’s rod close to first electromagnet (actually, instead of this second electromagnet there could be used the conductor wrapped around the rod as we described above in previous methods). The reason of this nearness is that magnetic field generally weakens directly proportional to distance’s third power and much time will be needed for decelerating Space Catapult’s rod if two electromagnets are far from each other.
This method probably will consume the most amount of energy but at the same time it will be the most effective because it does not depend on outer factors such as Earth’s magnetic field which is quite weak at the altitude of several ten thousand kilometers above the sea level.
Eventually, which methods for decelerating the Space Catapult’s rod would be the best? As we see each one of them have got their advantages and disadvantages. We can state that we should choose one of them according to spaceflight’s profile and goal. Particularly, if we decide to send the spacecraft into the deep space mission where especially high speed is necessary then in this case longer/more massive rod would be needed rotating at very high speed. Under such circumstance much energy will be needed for accelerating/decelerating the rod. We should also take into consideration the fact how frequently the Space Catapult will operate, in other words how mane payloads it will have to send into space per some certain amount of time, week/month and etc. If time interval between two following missions is relatively high then we should choose the method that will consume less energy and more time for decelerating the rod. On the contrary, if the Space Catapult has to send payloads very often then we should choose the method that will consume more energy and enable the rod to decelerate faster. In other words, we should find golden mean between consuming time and energy. We should also take into account how much energy supply will be produced at the Space Elevator’s counterweight (see Energy source placed on the Space Elevator’s counterweight) and what part of this energy can we spend for accelerating/decelerating the rod.
The rod’s rotations can be decelerated much faster than accelerated; the reason of it is that when accelerating the rod has got some sophisticated device as payload and generally unmanned spacecrafts are capable to high g-loads, but still for them some restrictions exist. After the payload is released at needed direction and speed, the rod can decelerate much faster because the rod itself is quite simple device without any complex and sophisticated details.
We can actually use several methods, such as the third one and then the first/fifth ones. This would be justified because of following reason: as we have already said when decelerating with the third/forth method the problem of weakness of the Earth’s magnetic field would occur, therefore much time would be necessary for described method(s) to perform and give us result. However, we should note that in the beginning when the rod rotates very quickly this method would still operate strong enough. This derives from Faraday's law of induction stating that “the electromotive force generated is proportional to the rate of change of the magnetic flux”. Therefore, in the beginning when the rod is rotating very quickly we can use the third/forth method(s) and when the rod significantly brakes we can apply to the first/fifth ones-they do not depend on Earth magnetic field. In other words, such approach would greatly help us in finding the golden mean between spending energy and time necessary for decelerating the rod.
And finally: after releasing the payload the Space Catapult’s rod can actually give us energy. More precisely, the electro motor itself can serve as electric generator also since we know that the same machine can operate as electric motor if it is fed with electricity and as generator for electricity if its rotor is rotated by other machines. Therefore after releasing the payload when the electro motor’s rotor is rotating very quickly it can give us energy, in result of which the rod will lose its kinetic energy and speed, as for generated energy it can be sent downwards to the Earth for our terrestrial needs (see the next section in this paper) or stored onboard the Space Elevator’s counterweight. This approach has got one substantial advantage: it does not imply additional mass (wrapped wire) that will cause problems because rotating heavier rod would consume more energy.
Energy source placed on the Space Elevator’s counterweight
As well-known, the Space Elevator’s cabin needs energy when moving along the cable and it can get it from the Earth by means of various ways, such as: laser beam, microwaves, through the cable itself and etc. On the other hand, Space Catapult also needs much energy for rotating the rod and for this purpose some energy source should be placed on the Space Elevator’s counterweight, presumably solar panels array. Doing this would demand additional funding and engineering work and this undertaking should be justified, so how can we prove that placing energy source on the counterweight would be necessary and useful? We should not forget that the energy generally could be simply transmitted from the Earth without carrying any material for energy source on counterweight; so we can justify this undertaking if we declare/prove that:
1. Energy source should be designed for both Space Elevator’s cabin and Space Catapult’s rod. We can imagine it as array of numerous solar panels producing enough energy for both above-mentioned constructions. For this purpose solar panels would be better solution than nuclear reactor because they do not need nuclear fuel to be carried from the Earth to counterweight, also they are capable for producing energy in a continuous mode. By the way this circumstance will enable us to send the payload to space by Space Catapult whenever we want without depending existence nuclear fuel at the counterweight.
2. Transmitting energy from the counterweight (“from above”) is better and advantageous than doing the same thing from Earth (“from below”). Indeed, when we try to transmit energy (laser or microwave beam) from the Earth to ascending cabin, the part of energy is inevitably lost and dispersed in the Earth’s atmosphere and (this is point of the question) this continues during the whole process of ascent. On the contrary, when transmitting the energy from counterweight to cabin the energy will be lost only on the little part of this voyage, more specifically until the cabin leaves the atmosphere (100 km in height) and when cabin leaves it the energy will be transmitted in vacuum without loss.
3. For receiving the energy from the Earth the huge solar panels (in case of laser beam) or antennas (in case of microwaves) will be needed to be mounted on the counterweight and this is additional mass and additional engineering work.
We think that these arguments given above are enough for shoving that placing energy source on the Space Elevator’s counterweight have advantages over transmitting energy from the Earth and as conclusion we can state that energy source on counterweight would serve both space transportation systems-Space Elevator and Space catapult.
As addition, we could use the energy produced on the counterweight for terrestrial needs also. Indeed, there have been developed numerous projects for receiving energy from space since 60-ies implying producing it by means of solar panels and then transmitting to the Earth. Combining all these three goals we can conclude that placing solar power plant on the Space Elevator’s counterweight would be triply useful and advantageous. In other words, when the Space Catapult and Space Elevator do not function, the energy produced on the counterweight should be directly transmitted to the Earth for our terrestrial needs and thus the idea of Space Elevator, Space Catapult and space power plant will be combined in one project.
Assembling the Space Catapult
Assembling in space such a huge structure as Space Catapult will not be an easy task from the technical point of view and definitely needs special engineering approach. Besides, we think that Space Catapult’s rod should be mounted at the Space Elevator’s counterweight separately from every other parts of the Space Catapult (e.g. electro motor and etc.); this circumstance is caused by rod’s gigantic sizes. More precisely, electric motor and plus any other equipments necessary for Space Catapult’s performance should be delivered to space by means of Space Elevator in a usual way; as for Space Catapult’s rod, it is a different matter and it should be delivered and mounted separately in the end.
Eventually, Space Catapult’s rod will be quite long, perhaps much more than 100 kilometers. It is obvious that delivering such a long rod as one single unit would be quite difficult task; also it is possible that due to its total mass the Space Elevator’s cabin will not be able to deliver such rod at all, but we have already mentioned that the Space Catapult may have the rod with various length; more precisely the rod may consist of two/more parts. In such case these parts should be delivered towards the counterweight separately and then assembled.
But the Space Elevator’s cabin can actually deliver the Space Catapult’s rod as one single unit in space. We think that this would depend only on rod’s mass. The Space Elevator’s lifting capacity is not well-known yet; however apparently it will not exceed one hundred metric tons and if Space Catapult’s rod is made of extra light material then cabin will be able to deliver it in space and in such case the following question will arise: how the cabin will deliver such a huge object in space without any damage?
This can be done by means of two cabins. Generally, Space Elevator’s conception implies only one cabin moving along the cable, but for some special purpose (like delivering Space Catapult’s rod in space) we can use the second cabin also that will descend downwards after finishing its job and will not participate in Space Elevator’s further performance. As for the process of delivering the rod, we can imagine it in a following manner: at first the rod will be placed horizontally on the Earth (thus it must be manufactured and then transported to the Space Elevator’s base station), then the Space Elevator’s first cabin will carry rod’s one end along the cable while the rod’s second end will be moved on the Earth so that the rod to take more and more vertical position. When the rod is in vertical position the second cabin will capture rod’s second end and will carry it in space. We think that without the second cabin it would be quite difficult for one cabin only to carry long/heavy rod because the rod may actually shake and crash to the Space Elevator’s cable and this is absolutely undesirable.
So, as we see in principle it looks to be quite easy, however the assembling may complicate due to rod’s length. In this case it would be better to carry not the rod as one single unit but its parts and then to assemble them in space in the following manner: two cabins will carry the first part as described above, when this part is delivered to space and temporarily hung at the cable the next two cabins will carry the second part that will be attached to the first one from below; the other parts will be delivered to space and assembled into the rod in the same way.
The obvious disadvantage of the above-described method is that each part needs two cabins on the Space Elevator’s cable, besides the humans will be needed for assembling the rod from these parts in the atmosphere’s upper layers; therefore we think that the first way-delivering the rod into space as one single unit still would be easier and more realistic; besides we should take into consideration the fact that if the rod is assembled the additional devices will be needed on the rod itself for joining these parts and this circumstance would lead to increasing the rod’s total mass and this is undesirable. See the image showing assembling process:
Whatever design/structure the rod has-assembled from several parts or as one single unit, it must be delivered to its destination-Space Elevator’s counterweight and must be fastened to electro motor’s own axis. But the problem is that the rod will be quite long and also the fact that Space Catapult’s electro motor will be placed at counterweight’s upper side (or at the lateral side if Space Catapult’s rod’s plane of rotation is parallel to Space Elevator’s cable, see Rod’s plane of rotation towards the Earth), so it will be necessary the rod coming from below to be moved to counterweight’s upper/lateral side, besides the rod should be docked with electro motor’s axis as accurately as possible. How is it possible to realize such complex engineering operation? Here we can indicate one possible theoretical way:
The rod will be parallel to Space Elevator’s cable when carried by cabin, but later the cabin’s mechanisms should rotate it so that the rod to be orthogonal to Space Elevator’s cable (this will not be necessary if Space Catapult’s rod’s plane of rotation is parallel to Space Elevator’s cable, see Rod’s plane of rotation towards the Earth), exactly in this position the rod should be delivered to counterweight, besides the rod when moving along the cable should be shifted a bit upwards (relative to the Earth) than the cabin itself. Under such conditions we will easily achieve docking the rod to electro motor’s own axis which from its side should have some trapping device (magnetic for example) to “catch” the rod and thus guarantee docking the rod to electro motor and finishing assembling the Space Catapult as a whole. But if the rod’s plane of rotation is parallel to cable then assembling process will be much easier because the ascending rod may directly dock to electro motor’s own axis. See the image showing this process:
We think that it would be useful if one Space Elevator is built specially for Space Catapult with its base station located on the land, not the ocean. This would be justified because transporting Space Catapult’s rod from its place of manufacture to Space Elevator’s base station should occur on the land by means of several transports simultaneously (due to rod’s great length), this will enable us to deliver the rod to its destination without any damage while this kind of operation is hardly possible on the water.
The technical aspects regarding the Space Catapult
As an example, we can try to calculate/ascertain all possible kinds of aspects regarding the rod with some certain mass and sizes, for example we can assume the Space Catapult has got 100 km length rod.
The circumference of the circle that this rod’s end will draw in space will be equal to 2πr=628 km. As we have already mentioned payload’s abilities for withstanding the g-load is restricted, so if the electromotor rotates the rod so that payload’s speed is equal to 50 km/sec (this means that it will take 12.56 seconds for the rod to make one complete revolution), in this case acceleration will be equal to 25 000 m/sec2, which is about 2550 g. The modern technologies enable to design the spacecraft that will withstand such acceleration, but what about the rod itself? Which material can be used for designing this rod, what will be its mass and how much energy and time will be needed for the rod to reach this velocity?
For manufacturing the rod we should choose the material with very low density and highest value of strength. Currently, the Carbon nanotubes are the best candidates for this purpose. What will the mass of the rod made of this material? This depends on width also and it should be as less as possible (otherwise the rod will be too heavy and too wide for transporting from manufacture place to Space Elevator’s base station and for delivering it to space by means of Space Elevator) but from the other hand the applied load will not let us to design very narrow rod.
Let’s assume that we intend to launch the payload with the mass of 10 000 kg (during calculation we will use SI system only). To clarify what kind of material will be able to withstand the acceleration we should calculate and then compare two values: the applied load and tensile strength. For calculating the first one we should multiply g-load (which we already know-2 550 g) to its mass-10 000 kg, we will get 25 500 000. As for calculating tensile strength, we should take its values (for Carbon nanotubes it varies from 11 000 MPa to 63 000, we will take some medium value-40 000 MPa) and multiply it to cross-section’s area, in our case rod is cylinder with circular cross-section. If radius of cross-section is 1 meters then its area is 3.14 square meters, multiplying this value to value of tensile strength (40 GPa as said) we will get 125 600 000 000 and this is significantly more than value of applied load-25 500 000. Of course, we should also take into consideration factor of safety which is generally equal to 2 and this indicates us that for safety the payload’s actual mass should be twice less but in our case as we see the rod will be able to accelerate the payload to above-mentioned speed. By the way, note that if that g-load 2 550 g is almost at the payload’s withstanding limit this is not serious problem for the rod itself (we have already seen that value of tensile strength is much more than value of applied load) and this is clear why: payload generally contains sophisticated equipments (electrical circuit, optics an etc.) that will not be able to withstand very high g-loads while the rod will be made of some continuous solid substance, Carbon nanotubes is this case and of course it will be able to withstand much higher g-loads.
What will be the mass of such rod? Knowing its volume (for this purpose its cross-section’s area 3.14 square meters should be multiplied to rod’s length-100 000 meters, we get 314 000 cubic meters) and taking the value of density (this also varies for Carbon nanotubes from 0.037 to 1.34 g/cm3, let’s take 0.1 g/cm3) we get rod’s mass as 31 400 000 kilograms. This is too heavy for Space Elevator’s modern concepts and for improving this situation we should either use many cabins for raising the rod as single unit or use nuclear energy for feeding the cabins instead of laser/microwave beams or deliver the rod’s parts separately in space and then assemble them (see Assembling the Space Catapult). But if some advanced substances are chosen for this purpose (for example Silica aerogel the density of which is about 1.9 mg/cm3, this is 50 times less than the density of the Carbon nanotubes taken above-0.1 g/cm3) than problem may be lightened in spite of the fact that their current tensile strength is quite low-16 kPa for the density of 0.1 g/cm3 7. So, we can conclude that we need the material with the density of Aerogels and tensile strength of Carbon nanotubes.
How much energy and time will be needed for the rod to accelerate from zero to desired speed-50 km/sec? The amount of rotational energy of the rotating rod can be calculated by the following formula: Kinetic Energyrotational= (1/2)*I*ω2
Where:
I=moment of inertia
ω=angular velocity
"I" depends on the shape of the mass under rotation. In the case of a uniform rod rotating from its end (axis of rotation is at the end of the rod) I = (m*L2)/3
“ω” = V/R, where V = tangential velocity and R = radius
In our case moment of inertia is equal to (31 400 000 kg*100 000 m2)/3=104 666 666 666 666 666 ω is equal to (50 000 m/sec)/100 000 m=0.5
So, Kinetic Energyrotational=(1/2)*104 666 666 666 666 666*(0.52)= 13 083 333 333 333 333.25 Joules
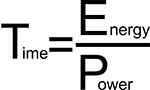
Now, how much time and what amount of solar panels will be needed for accelerating this rod? The amount of Solar constant near the Earth is approximately equal to 1300 W/m2 [8], with assuming that coefficient of efficiency of solar panels is roughly 20 % we get 260 Watts per square meters and we can easily link amount energy (that we have already calculated) and power with the time needed. Particularly, Energy is equal to Power’s multiplication to Time:
So, Time is equal to 13 083 333 333 333 333.25 Joules/260 Watts=50320512820512.8 seconds, or 1 595 652 years. If we take much more area for solar panels, for example 10 millions square meters then 0.1595652 years or approximately 58 days will be needed and we think that this is acceptable time span.
Actually, the time and energy will be needed a bit more for overcoming static friction in electro motor, for overcoming the rarified atmosphere’s resistance (we know that there no absolute vacuum in space), also we should take into consideration electric motors’ coefficient of efficiency that generally reaches 90-95 %, so some energy loss will occur here also.
Now, what will be the total mass of solar panels producing the energy for Space Catapult? This depends on mass/power ratio, in near future it is expected that very lightweight designs could likely achieve 1 kg/kW [8] or 0.260 kg/ 260 W (per 1 square meter), so if for rotating the Space Catapult 10 millions square meters of solar panels are used then their total mass would be equal to 2 600 000 kg. We think that it is too heavy for Space Elevator the mass of which is expected to be equal around several hundred metric tons. If so, we will have to use fewer amounts of solar panels and therefore increase the time needed for accelerating the payload’s speed from zero to designed one. This will not make problems if the rod is accelerated only once and then keeps its constant rotation-for this purpose less energy will be needed and the payload will have to reach the rod’s end by first method as described earlier in this paper (see Rod’s plane of rotation towards the Earth).
We also need to take into consideration the value of deflection when the rod will be delivered to space by means of Space Elevator (see Assembling the Space Catapult), in this case the thin and long rod will be bent due to its own weight and here we will try to calculate its value. This is quite complex problem that apparently cannot have an unambiguous solution because of many reasons, for example due to various temperatures in atmosphere’s different layers, various humidity and possible wind, but still we will try to calculate the value of Deflection that will occur in case when the rod’s one end is fastened to Space Elevator’s ascending cabin and the second end is fastened to the transport moving on the land, we discussed this option in above-mentioned section of our paper (see Assembling the Space Catapult). The inclination angle for the rod will vary from 0º (rod is transported horizontally on the ground) to 90º (Space Elevator’s cabins are carrying the rod to space) and here we will discuss some medium case when the rod is semi-elevated in the air, when the angle between rod and ground/cable is equal to 45º. On the engineers’ eFunda web-site there is online calculator that enables to receive the value of Deflection (actually that site gives different term for this-Displacement) [10]:
Here we need to enter the relevant values:
Length of beam, L: 100 000 meters
Line pressure load on beam, p: In our case this is the weight per meter length. As we have already mentioned the radius of the rod’s cross-section is 1 meter, so the volume of rod’s 1 meter-length part will be 3.14 cubic meter. In case of using Carbon nanotubes with above-mentioned density-0.1 g/cm3 the weight will be equal to 314 kg or 3 079 Newton. Since we have got the inclination of 45º we should multiply this value to cos45º- 0.707, so we get 2176 N/m.
Young's Modulus, E: This is equal to 1 000 GPa for Carbon nanotubes [11]
Distance from neutral axis to extreme fibers, c: In our case it is equal to the radius of the rod-1 meter
Moment of Inertia, I: It is equal to (pi*r4)/4, so it is equal to 0.785
According to these initial data the calculator returns extremely high value of Deflection, much higher than the length of the rod itself: -3.61 × 109 meters. This result shows us that with the current materials (Carbon nanotubes in our case) it is impossible to raise the rod as one single unit to space by means of Space Elevator and we need other materials with less density and more Young's Modulus (or the rod should be much thicker but this will lead to increasing its mass). Therefore, we have got two options: either we should deliver the parts of that rod and then assemble them in space (we have already discussed this option) or completely different technologies for manufacturing the rod should be developed. Particularly, it would be very good if it was possible to manufacture the rod in continuous mode in vertical position and then uninterruptedly directly to carry it to space by means of Space Elevator’s cabins. Under such approach there will be no Deflection and several cabins will be able to deliver the rod in space.
One note about transporting the rod from its place of manufacture to Space Elevator’s base station. We think that this process should be executed by many transports, in other words we are convinced that if the rod is carried by two trains only (or any other kind of transport) then the rod will continuously touch the ground since the Deflection occurs in any position-horizontal, inclined or vertical and this circumstance will lead to its damage, that’s why several transports will be needed to hold the rod at as many places as possible.
Stabilizing the counterweight
Stabilizing the Space Elevator’s counterweight is very important question during Space Catapult’s performance. Indeed, when the rod rotates it makes the imaginary circles in space and due to rod’s and payload’s masses the Space Catapult’s center of mass will be continuously shifted and if the counterweight is not somehow stabilized then it will make problems for accurate aiming to certain point at the celestial sphere. Also, if Space Catapult’s rod’s plane of rotation is parallel to Space Elevator’s cable then there will be the danger that the rod may actually hit the cable and cut it. To avoid these problems we need to apply to serious measurements.
First of all, the electro motor’s own axis can be quite long and this will diminish the chance to failure of the whole system. Actually, we are convinced that counterweight’s (where the electric motor will be placed) size will be quite large, mainly due to solar panels’ sizes and amount (this issue was discussed above), also the electromotor should be quite large and powerful to rotate the rod, and hence there will be enough distance between the rod and Space Elevator’s cable.
The second serious problem is that the center of gravity of the system is not at the center of rotation, therefore it will be necessary to balance the rotating system when the payload is attached and when it is released.
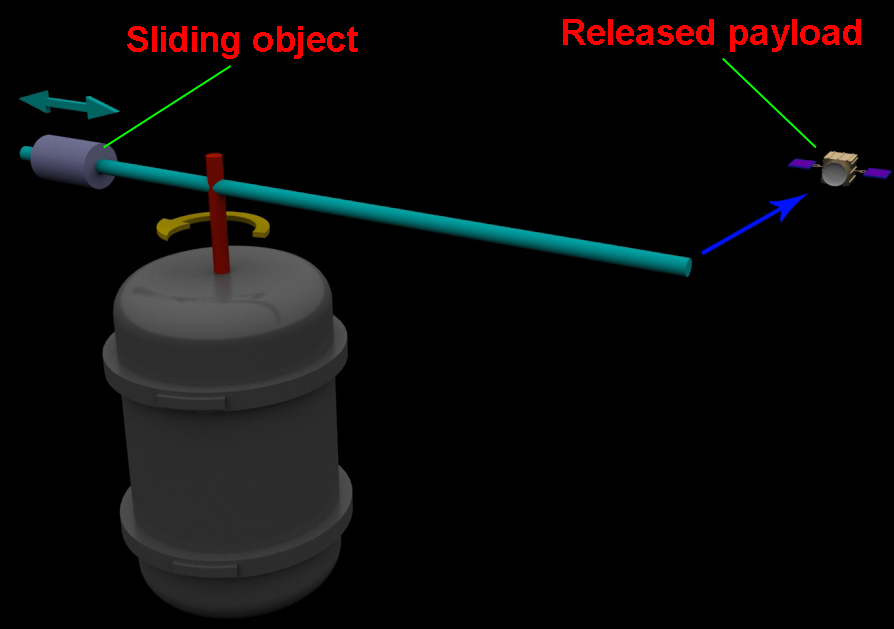
We think that the Space Catapult’s rod should not be deployed/directed to one side only but some counterweight of it should also exist. This is necessary since the unilaterally loaded (we mean the rod itself plus payload) rod will cause the counterweight to somersault. In other words, the rod should extend to other side and the moments of inertia of both sides should be the same as during rotating the rod as after releasing the payload when the rod still rotates. This is easily achievable if some additional, second payload is placed on the rod’s second end. Therefore, the Space Catapult will launch two payloads at the same time to the opposite directions but at various speeds if the second part/side of the rod is shorter.
How the second payload should be placed on the rod and should we really send two payloads? Until we have got balanced rod this problem does not arise but as soon as the Space Catapult releases the payload this balance will be violated, how it can be restored? There are two theoretical ways for achieving this: reducing the mass or reducing the length-with diminishing either one of them the moment of inertia will be decreased. We think that reducing the mass will be less practicable since this would require placing the second payload (spacecraft or anything else) on the rod’s second part and this cannot be done from the Space Elevator’s cabin-this is the easiest way for delivering the payload from Earth to Space Catapult’s rod; so we would have to (see Rod’s plane of rotation towards the Earth) put the second payload on the electro motor and then send it rod’s second part’s end. This is quite complicated task; therefore we can apply to second approach-put some sliding object that will immediately move to electromotor as soon as the spacecraft is released.
The next problem that may occur is that when the electro motor rotates the rod this motion will make the Space Elevator to rotate to the opposite direction. The same problem arises when helicopter’s primary blade’s rotation forces the helicopter to rotate to opposite direction and this possible rotation is annulled by tail rotor. We think that for balancing the counterweight the additional motor and rod should be installed and this rod should rotate to opposite direction and if their angular momentums are equal to each other, then their rotations will cancel each other. More precisely, the following equation should be fulfilled:
Where m is mass of the rod, v is angular speed and L is rod’s length, the numbers 1 and 2 refer to first and second rods correspondingly. For balancing both rods’ rotation the multiplication at both sides of the counterweight should be equal, by the way this circumstance enables us to use the second rod with shorter length and even with less mass but rotating at more angular velocity.
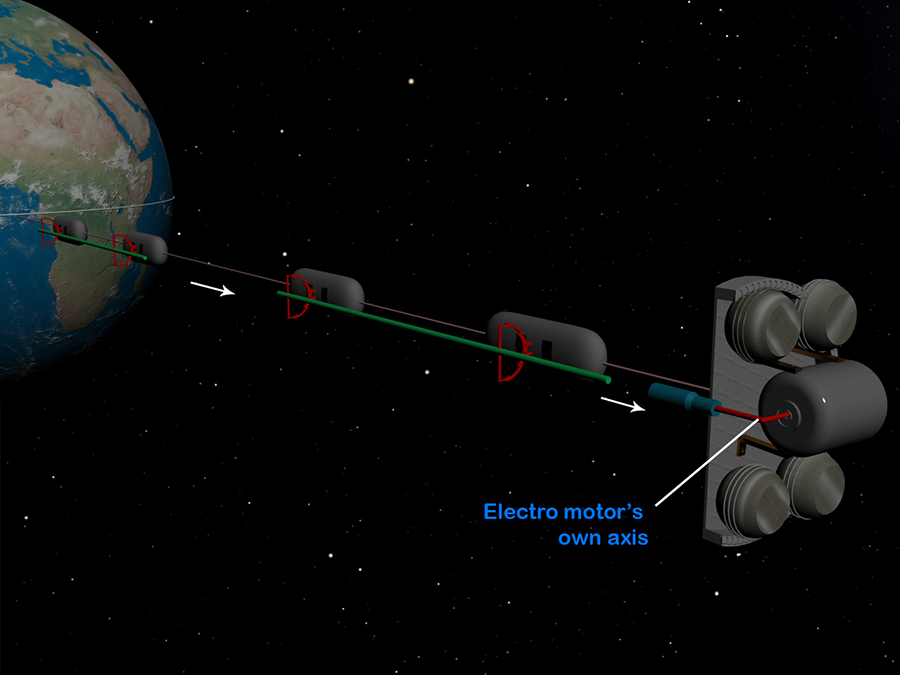
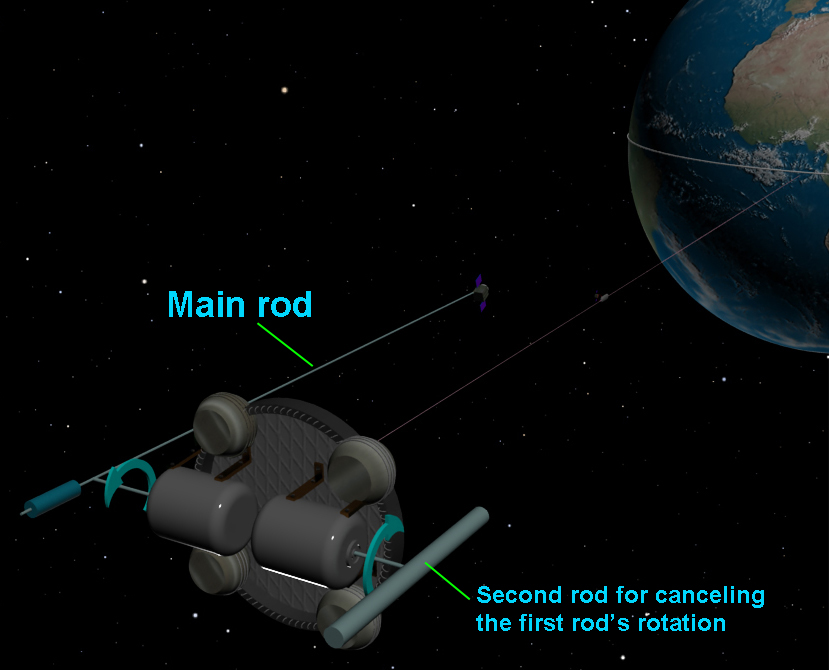
Such approach will effectively deal with other problem which will arise when the Space Catapult releases the payload(s), at this moment the second motor should instantly diminish its angular velocity to some certain level (an ordinary mechanical brakes could be used for this purpose), in this case angular momentums for both motors/rods will be equal again and Space Elevator’s counterweight will maintain its attitude in space. See the image below depicting the Space Catapult with two electro motors and rods:
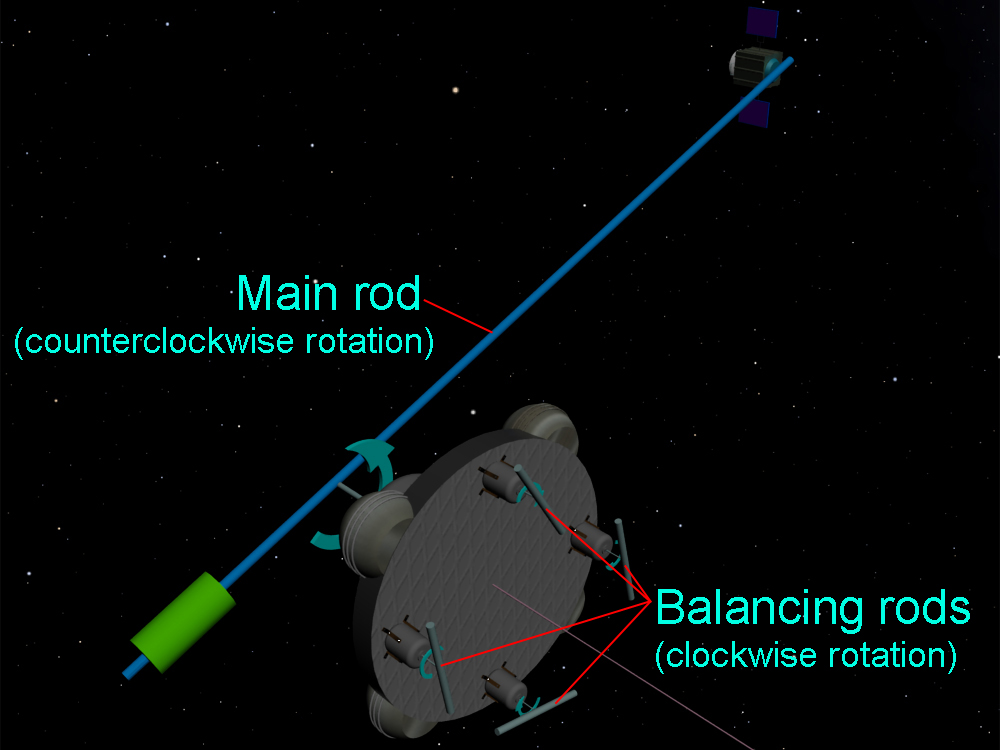
Such approach will justify itself if rod’s plane of rotation is parallel to Space Elevator’s cable, but if this plane is orthogonal to cable (see Rod’s plane of rotation towards the Earth) then the second/balancing electromotor cannot be placed under the counterweight because the cable will be cut when rod touches it. Therefore a bit different approach should used and we need to install two/four/eight electro motors with their own relatively shorter rods rotating to opposite direction. They should be placed at the counterweight’s lower side and on its edge (as we suppose the counterweight should be disc) so that their rods not to touch and cut Space Elevator’s cable. Also, total angular momentums from these motors should be equal to the angular momentum from upper motor and thus the counterweight will not rotate and the Space Elevator’s cable will not be twisted. This situation is presented below:
We think that the array of gyroscopes would be also very useful to be installed at the counterweight since they can maintain the attitude of the whole system and this is important for precise aiming to certain point at the celestial sphere. As for the energy required for gyroscopes’ performance it could be received from the array of solar panels which as a result will generally serve Space Catapult’s precise performance.
Space Catapult placed at Lagrangian points-the way for gaining subluminal speeds
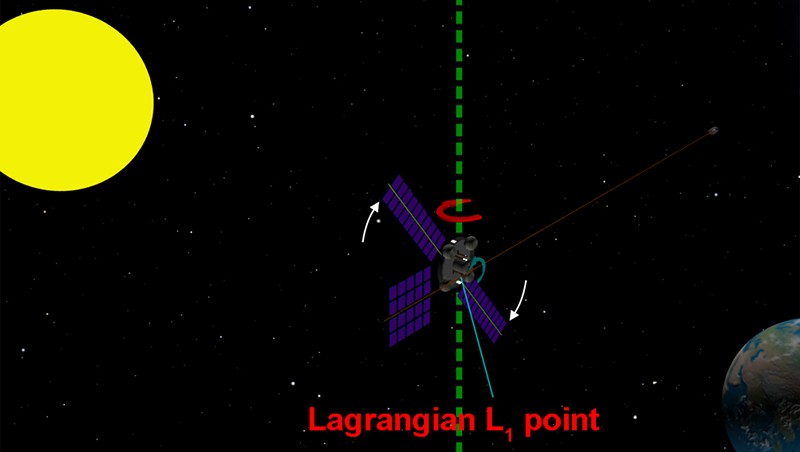
In our paper we discussed the Space Catapult based on the Space Elevator’s counterweight and concluded that this would be convenient when we intend to deliver the payload to space from the Earth. However, such Space Catapult cannot gain very high speeds and therefore we need to choose other way. It is obvious that we need to keep rod’s plane of rotation orthogonally relative to the Earth-Sun connecting line and hence we should place the rod on the celestial body which will be in synchronous rotation with the Sun but since there is no such body in the solar system we conclude that the Space Catapult for subluminal speeds (the speeds close to speed of light are in mind) should be placed at such point near the Earth where it will be easy to reach it from our planet and where the rotating rod will not hit the Earth and will be always at the same distance from the Sun to avoid the influence of its tidal forces. The examples of such places are Lagrangian L1 and/or L2 points at 1.5 million km away from the Earth. If the Space Catapult is placed at one of these points then its rod can be always orthogonal to the Sun in principle, at the same time it will never collide with the Earth and also it will be quite close to the Earth since 1.5 million km distance is very negligible in space.
We have got several notes regarding such approach. First, when we mentioned that the rod’s various parts can be at the same distance from the Sun this strictly speaking is not very true because the Sun can be referred as little point where its gravity “comes out” from while the rod is quite long and its initial part (placed at one of the Lagrangian points) will be attracted stronger than the utmost one (for equal attracting the rod should the arc with the same curviness as Sun’s surface and not straight line); but still this is better than to direct the rod exactly towards the Sun where the tidal forces will try to tear the rod. Second, the Space Catapult should be placed at Lagrangian L1 point which is closer to the Sun than L2 one and therefore receives by 4 % more energy per area from the Sun. Third, the rod should be in constant rotation, this requires much less energy than accelerating it from zero, then stopping it and accelerating it again. Fourth, the existence of the asteroid belt in the solar system between Mars and Jupiter will somehow restrict the actual length of the rod. Indeed, the Space Catapult should be placed at one of the Lagrangian points at 1 AU distance from the Sun while asteroid belt approximately lays at 2.7 AU, from the simple geometry it is obvious that the length of the rod almost reaching the asteroid belt can be approximately equal to 390 million km, and if the rod is longer then it may simply hit any asteroid within that belt. For 390 million km length rod and for 100 000 m/sec2 acceleration at rod’s end (where the payload will be attached) the maximal speed that the spacecraft can gain will be approximately equal to 200 000 km/sec (two thirds of the speed of light) and this can be considered as enough for practical interstellar spaceflight. Fifth, the spacecraft should be directly put on the rotating rod’s initial end (near electromotor) and then slide towards the other end with its own rocket engines. To achieve this, the spacecraft will have to cover relatively less distance on the rod and then rod’s circular motion will accelerate the spacecraft further-we have already mentioned this in this paper when speaking about deploying the Lunar Space Catapult. This action-putting the spacecraft on the rod will not be difficult since rod’s angular velocity will be quite low due to rod’s huge length, particularly for 400 million km length rod and for 200 000 km/sec linear speed the rod’s angular velocity will be 0.0000796 revolutions/sec.
We have already mentioned that to avoid the destructive influence of the Sun’s tidal forces the rod’s plane of rotation should be orthogonal to the Earth-Sun connecting line. By the way, note that under such approach we may have to wait one year until the Lagrangian Space Catapult occupies the relevant position towards the certain point at the celestial sphere where the spacecraft should be sent to. But from the other hand it would be useful if it is feasible to rotate this whole structure around the imaginary axis directed towards the ecliptic poles (depicted as faint green dash line on the image above), the reason if this is the possible danger when the rotating rod may hit Mars or asteroids that orbit around the Sun closer than 2.7 AU distance (for example 433 Eros or 1036 Ganymed), hence for avoiding such undesired collision the Lagrangian Space Catapult should be slightly rotated by several degrees clockwise/counterclockwise so that the rod not to collide with any celestial object. We are convinced that rotation by several degrees will be absolutely enough measurement due to rod’s gigantic length and relatively less sizes of the celestial objects in the solar system.
The next issue that we should discuss refers to stability of the Lagrangian Space Catapult placed at L1 point. As we see this structure will have enormously gigantic size while the Lagrangian point is relatively little mathematical one in space, so what can be done to be convinced that this structure will remain at that point and do not shift aside? The body placed at one of the Lagrangian points is affected by other celestial objects’ gravity and therefore for achieving the balance the rod needs to have the counterweight with more mass if it (counterweight) is shorter. As we clearly see the rod needs the counterweight for two reasons: not to let the Space Catapult somersault and for maintaining it at the L1 point. We think that it would be very useful if the arrays of solar panels act as counterweight since exactly they can give us energy for rotating the rod. Also, we need the second, shorter, perhaps less massive but faster-rotating rod (again-solar panel arrays) the opposite rotation of which would cancel first rod’s rotation, this issue was discussed in this paper. These arrays of solar panels are depicted on the image shown above.
How such a gigantic structure as Lagrangian Space Catapult can be assembled in space? In our paper we discussed the possible ways for delivering the rod from the Earth to the Space Elevator’s counterweight, now we will try to show that it is possible in principle to assemble the extra-long rod in space.
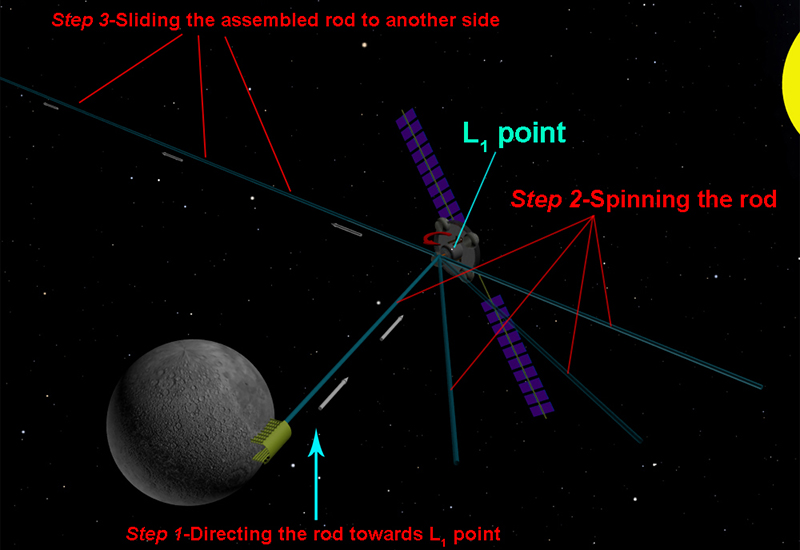
If it is possible from the technical point of view to manufacture extra-long rod then we can use this approach and make 1.5 million km length rod (this is the distance between the Earth and Lagrangian L1/L2 point) that will be mechanically directed to the base station at L1 point. The capturing devices there will catch the rod and attach it to the electro motor’s shaft after which the rod should be spun by 90º so that it to be orthogonal to Earth-Sun connecting line (for this purpose the additional mechanisms will be needed), this spin is necessary because L1 point is located on the Earth-Sun connecting line (that is towards the Sun if we look from the Earth) and when directing the rod from the Moon it will lay along this line while we need across. After this the rod should be slid to another side and then the next rod should be directed to the Lagrangian Space Catapult where it will be attached to the previous rod and etc. In other words, the extra-long rod will be assembled from one side and its length will “grow” from this side to other one, this is necessary because the distance between Moon (the rod should be manufactured exactly there and not on the Earth due to our planet’s relatively more gravity, atmosphere and problematic space debris belt around it) and L1 point is constant and rod’s parts cannot be more. Due to whole rod’s and its parts’ lengths (400 million and 1.5 million km correspondingly) we think that about 260-270 such operations will be needed to finish assembling the rod (400/1.5). The process of assembling the Lagrangian Space Catapult is shown on the image below:
Conclusion
As we have seen, for leaving the Solar system and reaching the remote celestial bodies (stars, nebulas) there is no need to develop advanced and complicated technologies that mostly are not capable for gaining extra high velocities nevertheless. In any case, until the Space Elevator is really built (scheduled for construction by 2031) we have got much time for developing the idea of Space Catapult in technical aspect, like finding appropriate materials for the rod, perfect the ways how the Space Catapult can be assembled in space and etc. The concept of Space Catapult itself is the easiest one, does not need developing neither complex and sophisticated technologies, nor some exotic methods (such as Gravitoelectromagnetic toroidal launchers, Antimatter rocket and etc.) and can be easily implemented in near future; in other words the Space Catapult is not some sophisticated structure that would need profound science research and the fact that it will enable us to gain whatever high speed will justify its developing and building by the humankind. As for other technologies like Ion Drive, they could be used by the spacecraft during flight for other purposes, for example for correcting/changing the flight direction.
References:
1. http://en.wikipedia.org/wiki/Space_Elevator 2. http://www.isec.info/index.php?option=com_content&view=article&id=14&Itemid=9 3. http://www.space-track.org/perl/geo_report.pl (provided data updates regularly, registering is needed) 4. http://www.oosa.unvienna.org/pdf/reports/ac105/AC105_720E.pdf page 24 (data as at 21 August, 1997) 5. http://www.amostech.com/ssw/presentations/Session7/S7-1Molotov.pdf page 16 6. http://www.esa.int/SPECIALS/ESOC/SEMN2VM5NDF_mg_1_s_b.html 7. http://eetd.lbl.gov/ecs/aerogels/sa-physical.html 8. http://www.pmodwrc.ch/pmod.php?topic=tsi/composite/SolarConstant 9. http://www.you.com.au/news/2005.htm, http://www.spacedaily.com/news/ssp-03b.html 10. http://www.efunda.com/formulae/solid_mechanics/beams/casestudy_display.cfm?case=simple_uniformload 11. http://en.wikipedia.org/wiki/Young%27s_modulus